
The symbol for positive edge triggered T flip flop is shown in the Block Diagram. It has only input denoted by T as shown in the Symbol Diagram. Toggle flip flop is basically a JK flip flop with J and K terminals permanently connected together. This will set the latch and Q n+1 = 1 and Q n+1 bar = 0 irrespective of the present state. If E = 1 and D = 1, then S = 1 and R = 0. Hence irrespective of the present state, the next state is Q n+1 = 0 and Q n+1 bar = 1. Block Diagram Circuit Diagram Truth Table Operation S.N. This problem is avoid by SR = 00 and SR = 1 conditions. Hence S = R = 0 or S = R = 1, these input condition will never appear. S and R will be the complements of each other due to NAND inverter. Due to this data delay between i/p and o/p, it is called delay flip flop. The input data is appearing at the output after some time. The master slave flip flop will avoid the race around condition.ĭelay Flip Flop or D Flip Flop is the simple gated S-R latch with a NAND inverter connected between S and R inputs. This avoids the multiple toggling which leads to the race around condition. So it does not respond to these changed outputs. But since clock = 0, the master is still inactive. These changed output are returned back to the master inputs. So S and R also will be inverted.Ĭlock = 0 − Slave active, master inactive.

Therefore outputs of the slave become Q = 1 and Q bar = 0.Īgain clock = 1 − then it can be shown that the outputs of the slave are stabilized to Q = 1 and Q bar = 0.Ĭlock = 1 − Master active, slave inactive. That means S = 1 and R =0.Ĭlock = 0 − Slave active, master inactive. Therefore outputs of the master become Q 1 = 1 and Q 1 bar = 0. Thus we get a stable output from the Master slave.Ĭlock = 1 − Master active, slave inactive. Hence with clock = 0 and slave becoming active the outputs of slave will remain Q = 0 and Q bar = 1. Therefore even with the changed outputs Q = 0 and Q bar = 1 fed back to master, its output will be Q1 = 0 and Q1 bar = 1. Therefore outputs of the slave become Q = 0 and Q bar = 1.Īgain clock = 1 − Master active, slave inactive. That means S = 0 and R =1.Ĭlock = 0 − Slave active, master inactive. Therefore outputs of the master become Q 1 = 0 and Q 1 bar = 1. Therefore outputs will not change if J = K =0.Ĭlock = 1 − Master active, slave inactive. But since the S and R inputs have not changed, the slave outputs will also remain unchanged. When clock = 0, the slave becomes active and master is inactive. Circuit Diagram Truth Table Operation S.N. Whereas when clock = 0 (low level) the slave is active and master is inactive. Hence when the clock = 1 (positive level) the master is active and the slave is inactive. But due to the presence of the inverter in the clock line, the slave will respond to the negative level. Master slave JK FF is a cascade of two S-R FF with feedback from the output of second to input of first.
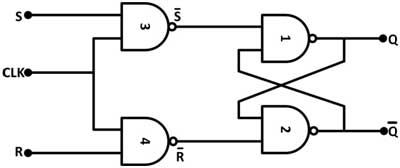
Hence the Race condition will occur in the basic NAND latch. This is the reset condition.Īs S = 1, R = 1 and E = 1, the output of NAND gates 3 and 4 both are 0 i.e. Hence output of S-R NAND latch is Q n+1 = 1 and Q n+1 bar = 0. R' = 1 and E = 1 the output of NAND-4 i.e. Since S' and R' are the input of the basic S-R latch using NAND gates, there will be no change in the state of outputs. If S = R = 0 then output of NAND gates 3 and 4 are forced to become 1. In short this circuit will operate as an S-R latch if E = 1 but there is no change in the output if E = 0. For this, circuit in output will take place if and only if the enable input (E) is made active. It is also called as level triggered SR-FF. It is basically S-R latch using NAND gates with an additional enable input. Flip flop is said to be edge sensitive or edge triggered rather than being level triggered like latches.

Block diagram Flip Flopįlip flop is a sequential circuit which generally samples its inputs and changes its outputs only at particular instants of time and not continuously. This type of circuits uses previous input, output, clock and a memory element. But sequential circuit has memory so output can vary based on input.

Hence the previous state of input does not have any effect on the present state of the circuit. The combinational circuit does not use any memory.


 0 kommentar(er)
0 kommentar(er)
